Answer:
(1, 6) and (-1, 6)
Explanation:
Well, we can just solve for y in one of the equations and substitute it into the other equation.
Original equation:
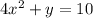
Subtract 4x^2 from both sides

Original Equation:

Now substitute in -4x^2+10 as y
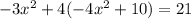
Distribute the 4
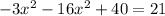
Subtract 21 from both sides and combine like terms
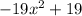
Factor out -19
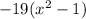
Rewrite using difference of squares
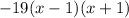
Zeroes at :x=-1 and x=1, since that makes one of the factors zero, thus making the entire thing zero and anything * zero = zero
Now let's just plug in these two values to find the y-values. We can use either equation
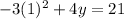
Simplify
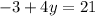
Add 3 to both sides

Divide both sides by 4
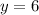
We know that -1, will yield the same thing, since (-1)^2=1, so it's going to have the same y-value of 6.
(1, 6) and (-1, 6)