Answer:
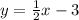
The answer is the same line as given in the question.
Explanation:
Hello!
Slope-intercept Form:

- y = output
- m = slope
- x = input
- b = y-intercept
Given our Line:
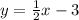
- slope =
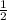
- y-intercept =
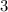
Parallel lines have the same slope but a different y-intercept, so the second line should have a slope of
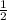 .
.
To find the y-intercept, we plug in the x and y values from the point into a blank equation with the slope and solve for b.
The equation is
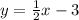 , hence the same line.
, hence the same line.