Question

Expand(x-3)^5 using Pascal’s triangle. show all the steps

Answer 1

Pascal's triangle is attached to the answer.

The expansion of the Newton's binomial for the fifth degree is written as follows:

`(a+b)^5=\dbinom{5}{0}a^5+\dbinom{5}{1}a^4b+\dbinom{5}{2}a^3b^2+\dbinom{5}{3}a^2b^3+\dbinom{5}{4}ab^4+\dbinom{5}{5}b^5,`

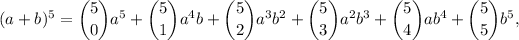
where
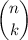`\dbinom{n}{k}` is the binomial coefficient (in the course of combinatorics it is proved that it is equal to the set of all
`k`-combinations of a set
`n`):

`\dbinom{n}{k}=C_n^k`

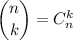
Let's choose the 5th row of the Pascal's triangle (with the second coefficient equal to five, a string with only the number 1 is considered null). The numbers written in this row correspond to the binomial coefficients:

`\dbinom{5}{0}=1\\\dbinom{5}{1}=5\\\dbinom{5}{2}=10\\\dbinom{5}{3}=10\\\dbinom{5}{4}=5\\\dbinom{5}{5}=1`

`(x-3)^5=\\=x^5+5x^4 \cdot (-3)+10x^3 \cdot (-3)^2+10x^2 \cdot (-3)^3+5x \cdot (-3)^4+1 \cdot (-3)^5=\\=x^5-15x^4+90x^3-270x^2+405x-243`

A screenshot is attached to the answer with checking the result on a computer.

If you do not understand something, you can ask, I can explain.