Question

Log 2 base 5 = 0.431 Log 3 base 5 = 0.683

Answer 1

approximately 0.25193

Explanation:

Ok so, there is something known as the change of base formula, which is used to change any logarithm, into another valid base. This can be expressed as:
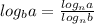`log_ba=(log_na)/(log_nb)` where n=a valid base.

This is particularly useful when evaluating logarithms using a calculator, when that calculator does not allow you to set the base, but rather it only has base 10, and base e/natural log

So, generally when that's the case, we rewrite the logarithm as:
`log_ba=(log(a))/(log(b))`

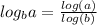
Using the change of base formula, we get the equation:
`(log(1.5))/(log(5))` using a calculator to evaluate the numerator and denominator, this is approximately:
`(0.17609)/(0.69897)`, now using a calculator to further evaluate this fraction, we approximately get:
`0.25193`

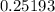
If you want a proof for this equation, you can read the stuff below:

Ok, you need to know the logarithmic identities, and in particular the logarithm of a power rule, which essentially states:
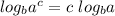`log_ba^c=c\ log_ba` which goes both ways, so you can combine them or separate them.

The reason this works, is because of the power of a power exponential rule which essentially states:
`(x^a)^b=x^(a*b)`

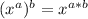
So let's just start with a basic logarithm:
`let\ x=log_ba\implies b^x=a`

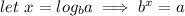
Since the two sides are equal, if we raise both sides to an exponent, they should remain equal. I'll represent this exponent as the variable "c"

`(b^x)^c=a^c`

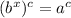
Using the power of a power exponent rule, we can rewrite this as:

`b^(x*c)=a^c`

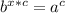
Now if we convert it back to logarithmic form, we get:

`log_ba^c=x*c`

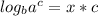
And remember what the "x" variable represented? It's the logarithm! So let's substitute that back in

`log_ba^c=c*log_ba`

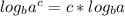
All of the logarithmic identities are deeply rooted in the exponent identities, since the logarithm literally represents the exponent, so these two are intertwined.

Ok so now getting that out of the way, let's start with another basic logarithm:

`log_ba`

Now let's multiply it by
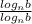`(log_nb)/(log_nb)` where n=a valid base. Since the numerator and denominator are the same, we're just multiplying by 1, so we're not actually change the value, just how it's represented

`(log_ba)/(1)*(log_nb)/(log_nb)=(log_ba\ *\ log_nb)/(log_nb)`

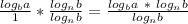
Now remember the logarithmic identity we just proved? We can move the logarithmic to the "b" as an exponent, since the identity goes two ways, so we get the following expression:

`(log_nb^(log_ba))/(log_nb)`

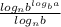
Now if you stop to think for a moment, you'll realize that
`log_ba` really just represents the exponent, that "b" needs to be raised to, to get the value "a". In this new form, we're raising the "b" to
`log_ba`, so we can simplify the:
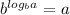`b^(log_ba)=a` . This gives us the following fraction:

`log_ba=(log_na)/(log_nb)`

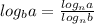
This formula works for any valid base.