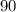Answer:
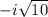 (-i root 10)
(-i root 10)
Explanation:
1. Rewrite the equation:
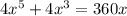 | divide by
| divide by
 ,
,
 is assumed not being zero
is assumed not being zero
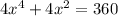 | rearrange and divide by
| rearrange and divide by

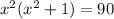
2. Substitute
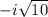 , to the equation:
, to the equation:

calculate that
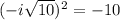 , and substitute to find
, and substitute to find
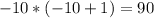
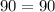 , and the equation holds.
, and the equation holds.
3. We can substitute
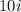 ,
,
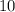 and
and
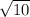 , too, and find:
, too, and find:
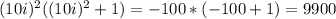 doesn't equal
doesn't equal
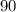 ,
,
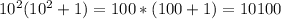 , doesn't equal
, doesn't equal
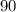
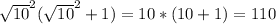 that isn't equal to
that isn't equal to