Please help me with my homework \bf{(x+9)^5} Thank you

Question

Please help me with my homework


`\bf{(x+9)^5}`

Thank you

Answer 1

x⁵+ 45x⁴+ 810x³+ 7290x²+ 32805x +59049

Explanation:

Greetings !

Given expression

`(x + 9) {}^(5)`

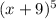
write 5 as a sum

`(x + 9) {}^(3 + 2)`

`use \: a {}^(m + n) = a {}^(m) * a {}^(n) to \: expand \: the \: expression.`

`(x + 9) {}^(3) * (x + 9) {}^(2)`

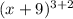
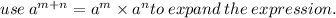
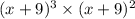
Use (a+b)³=a³+3a²b+b³ to expand the expression

`(x {}^(3) + 27x {}^(2) + 243x + 729) * (x + 9) {}^(2)`

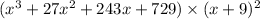
Use (a+b)²=a²+2ab+b² to the second expression to expand it

`(x {}^(3) + 27x {}^(2) + 243x + 729) *(x {}^(2) + 18x + 81)`

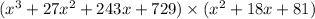
Finally, simplify the expression gives

`x {}^(5) + 45x {}^(4) + 810x {}^(3) + 7290x {}^(2) + 32805x + 59049`

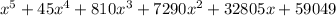
Hope it helps!

Answer 2

`\sf x^5 + 45x^4 + 810x^3 + 7290x^2 + 32805x + 59049`

Given expression:

`\bf (x+ 9)^5`

Use Binomial expression to completely simplify the following expression.

Binomial expression formula:

`\sf \large \text{ $ \sf (x+y)^n = \ ^n C_0 x^n y^0 + ^n C_1 x^(n-1) y^1+^n C_2 x^(n-2) y^2 +... + ^n C_n x^0 y^n $}`

Solving steps:

`\sf \large \text{ $ \sf (x+9)^5 $}`

expanding:

`\sf \ ^5 C_0 (x)^5 (9)^0 + ^5 C_1 (x)^(5-1) (9)^1+ ^5 C_2 x^(5-2) (9)^2 +^5 C_3 x^(5-3) (9)^3 +^5 C_4 x^(5-4) (9)^4 + ^5 C_5 x^(5-5) (9)^5`

calculating:

`\sf x^5 + 45x^4 + 810x^3 + 7290x^2 + 32805x + 59049`