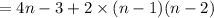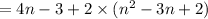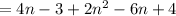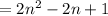Answer:
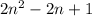
Explanation:
let ‘n’ be the number of the figure.
For n = 2 :
The number of the squares of the second figure :
= (the number of the squares of the middle/horizontal row) + (the number of the remaining squares)
= (2×2−1) + 2×(1+2×0)
= (3) + 2×(1)
= 3 + 2
= 5
For n = 3 :
The number of the squares of the third figure :
= (the number of the squares of the middle/horizontal row) + (the number of the remaining squares)
= (2×3−1) + 2×[(1+2×0) + (1+2×1)]
= (5) + 2×[(1) + (3)]
= 5 + 2×[4]
= 5 + 8
= 13
For n = 4 :
The number of the squares of the fourth figure :
= (the number of the squares of the middle/horizontal row) + (the number of the remaining squares)
= (2×4−1) + 2×[(1+2×0) + (1+2×1)+ (1+2×2)]
= (7) + 2×[(1) + (3) + (5)]
= 7 + 2×[9]
= 7 + 18
= 25
For n (n ≥ 2) :
The number of the squares of the nth figure :
= (the number of the squares of the middle/horizontal row) + (the number of the remaining squares)
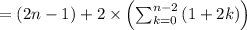
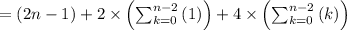
![= (2n-1) +2(n-1)+4* [(n-1)/(2)(0+(n-2))]](https://img.qammunity.org/2023/formulas/mathematics/high-school/oui8pkbypqum5p2ic0ch4oig3m9nf4hiy5.png)
![= (2n-1) +(2n-2)+4* [(n-1)/(2)(n-2)]](https://img.qammunity.org/2023/formulas/mathematics/high-school/ej93da2qcvx8p3iue64dq9mwffysi8c7kx.png)