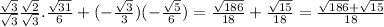Question

Q13
Please help me solve this….

Answer 1

Choice C

`(√(186)+√(15))/(18)`

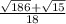
Explanation:

The quadrant in which an angle lies determines the signs of the trigonometric functions sin, cos and tan

If an angle Θ lies in quadrant IV, cos(Θ) is positive and both sin(Θ) and tan(Θ) are negative

Two of the trigonometric identities we can use are

1.
`\sin^2(\theta) + cos^2(\theta) = 1` and

2.
`\cos(A-B) = \cos A\cos B - \sin A\sin B`

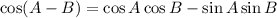
Using identity 1, we can solve for cos(s) and cos(t)

`sin(s)=-(√(3))/(3), sin^(2)(s)=(3)/(9)=(1)/(3)\\cos^(2)(s)=1-sin^(2)(s)=1-(1)/(3)=(2)/(3); cos(s)=\pm\sqrt{(2)/(3)}\\\\`

`sin(t)=-(√(5))/(6), sin^(2)(t)=(5)/(36)cos^(2)(t)=1-sin^(2)(t)=1-(5)/(36)=(31)/(36);cos(t)=\pm(√(31))/(6)`

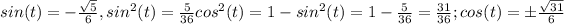
Since both angles lie in quadrant IV, both cos(s) and cos(t) must be positive so we only consider the positive signs of both values

Using identity 2, we can solve for cos(s-t)

`cos(s-t)=cos(s)cos(t)+sin(s)sin(t)=(√(2))/(√(3)).(√(31))/(6)+(-(√(3))/(3))(-(√(5))/(6))`

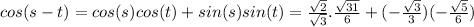
Multiplying numerator and denominator of the first term by
`√(3)` gives us the final expression as

`(√(3))/(√(3))(√(2))/(√(3)).(√(31))/(6)+(-(√(3))/(3))(-(√(5))/(6))=(√(186))/(18)+(√(15))/(18)= (√(186)+√(15))/(18)`