Question

Why does it make sense that the outputs of a geometric sequence represent an exponential function

Answer 1

Explanation:

Ok so a geometric sequence is essentially just multiplying out the probability of independent events occurring.

You've likely calculated the probability of two independents occurring as:
`P(A\cap B)=P(A)*P(B)`

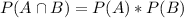
You can extend this out to:

`P(A\cap B\cap C\cap D...)=P(A)*P(B)*P(C)*P(D)...`

So if we want to find the probability of independent events occurring we just multiply them out.

This is where we get the geometric sequence formula:

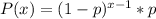`P(x)=(1-p)^(x-1)*p` where p=probability of success, and 1-p = probability of failure, and x=amount of trials.

P(x) just basically outputs the probability of needing "x" trials, to find one success.

The formula makes sense, since the failure is occurring "x-1" times, and the success is only occurring one time.

The probability of failure is (1-p), since the total probability is just 1, so the probability of failure is (1-p)..

So we're just multiplying the independent event of failure times it self (x-1) times, and multiplying it by the independent event of success which occurs one time in a geometric distribution.