Question

Dividing sin²+ cos²0 = 1 by
yields 1 + cot² Ø = csc²0

Answer 1

Answer: sin²∅

Explanation: If you divide each term by sin squared theta, sin²∅/sin²∅ = 1, cos²∅/sin²∅ = cot²∅, and 1/sin²∅ = csc²∅, which is your result.

Answer 2

sin²θ

Explanation:

To determine what we need to divide
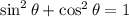`\sin^2 \theta+\cos^2 \theta=1` by to yield
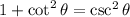`1+\cot^2 \theta=\csc^2\theta`, compare equations:

`\textsf{Equation 1}: \quad \sin^2 \theta+\cos^2 \theta=1`

`\textsf{Equation 2}: \quad 1+\cot^2 \theta=\csc^2\theta`

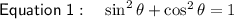
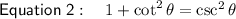
If we divide a term by itself, it will always yield 1.

Therefore, divide each term in the first equation by sin²θ:

`\implies (\sin^2 \theta)/(\sin^2 \theta)+(\cos^2 \theta)/(\sin^2 \theta)=(1)/(\sin^2 \theta)`

`\implies 1+(\cos^2 \theta)/(\sin^2 \theta)=(1)/(\sin^2 \theta)`

`\boxed{\begin{minipage}{4 cm}\underline{Trigonometric Identities}\\\\$\cot \theta=(\cos \theta)/(\sin \theta)\\\\\csc \theta=(1)/(\sin \theta)$\\\end{minipage}}`

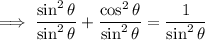
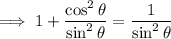
Use the trigonometric identities for cot and cosec:

`\implies 1+(\cos^2 \theta)/(\sin^2 \theta)=(1)/(\sin^2 \theta)`

`\implies 1+\left((\cos \theta)/(\sin \theta)\right)^2=\left((1)/(\sin \theta)\right)^2`

`\implies 1+(\cot \theta)^2=(\csc \theta)^2`

`\implies 1+\cot^2 \theta=\csc^2 \theta`

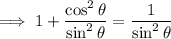
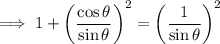
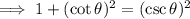
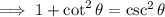
Thus proving that sin²θ + cos²θ = 1 should be divided by sin²θ to yield

1 + cot²θ = csc²θ.