Question

Help please! anyone know how to graph this

Answer 1

The grpah should help!

Answer 2

See attached for graph of the given function.

Explanation:

Vertex form of a quadratic function

`f(x)=a(x-h)^2+k`

where:

• (h, k) is the vertex.
• a is some constant to be found.
  If a>0 the parabola opens upwards.
  If a<0 the parabola opens downwards.

Given function:

`g(x)=-(1)/(5)(x+5)^2-2`

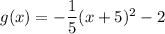
Vertex

Comparing the given function with the vertex formula:

`\implies h=-5`

`\implies k=-2`

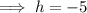
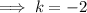
Therefore, the vertex of the parabola is (-5, -2).

As a<0, the parabola opens downwards. Therefore, the vertex is the maximum point of the curve.

Axis of symmetry

The axis of symmetry is the x-value of the vertex.

Therefore, the axis of symmetry is x = -5.

y-intercept

To find the y-intercept, substitute x = 0 into the given function:

`\implies f(0)=-(1)/(5)(0+5)^2-2=-7`

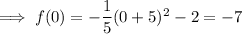
Therefore, the y-intercept is (0, -7).

x-intercepts

To find the x-intercepts, set the function to zero and solve for x:

`\implies -(1)/(5)(x+5)^2-2=0`

`\implies -(1)/(5)(x+5)^2=2`

`\implies (x+5)^2=-10`

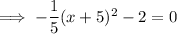
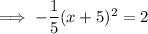
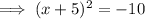
As we cannot square root a negative number, the curve does not intercept the x-axis.

Additional points on the curve

As the axis of symmetry is x = -5 and the y-intercept is (0, -7), this means that substituting values of x in multiples of 5 either side of the axis of symmetry will yield integers:

`\implies f(-10)=-(1)/(5)(-10+5)^2-2=-7`

`\implies f(5)=-(1)/(5)(5+5)^2-2=-22`

`\implies f(-15)=-(1)/(5)(-15+5)^2-2=-22`

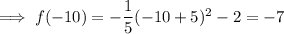
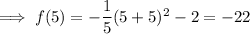
Therefore, plot:

• vertex = (-5, -2)
• y-intercept = (0, -7)
• points on the curve = (-10, -7), (5, -22) and (-15, -22)
• axis of symmetry: x = -5

Draw a smooth curve through the points, using the axis of symmetry to ensure the parabola is symmetrical.