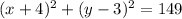Question

Find an equation of the circle that has center (-4,3) and passes through (6,-4).

Answer 1

`(x+4)^2+(y-3)^2=149`

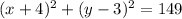
Explanation:

The equation of a circle is
`(x-h)^2+(y-k)^2=r^2` where
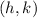`(h,k)` is the center of the circle and
`r` is the radius of the circle.

Given that
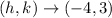`(h,k)\rightarrow(-4,3)` and it passes
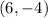`(6,-4)`, their distance between each other must the radius of the circle, so we can use the distance formula to find the radius:

`d=√((y_2-y_1)^2+(x_2-x_1)^2)\\\\d=√((-4-3)^2+(6-(-4))^2)\\\\d=√((-7)^2+10^2)\\\\d=√(49+100)\\\\d=√(149)`

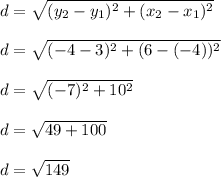
Therefore, if the length of the radius is
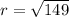`r=√(149)` units, then
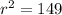`r^2=149`, making the final equation of the circle
`(x+4)^2+(y-3)^2=149`