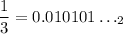Question

When using bits to represent fractions of a number, can you create all possible fractions?.

Answer 1

Every rational number has a base-2 representation, but only the ones with denominators that are powers of 2 will require a finite number of bits to fully represent it.

For example,

`\frac12 = 1\cdot2^(-1) = 0.1_2`

`\frac14 = 1\cdot2^(-2) = 0.01_2`

`\frac34 = \frac12 + \frac14 = 0.11_2`

`(1023)/(1024) = 1 - \frac1{2^(10)} = 1_2 - 0.0000000001_2 = 0.1111111111_2`

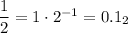
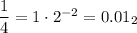
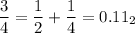
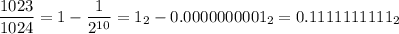
whereas a number whose denominator contains anything else like 1/3 will need an infinite number of bits to represent it exactly.

`\frac13 = \frac1{2^2} + \frac1{12} = \frac1{2^2} + \frac1{2^4} + \frac1{48} = \frac1{2^2} + \frac1{2^4} + \frac1{2^8} + \frac1{192}`

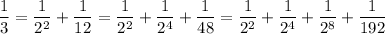
and so on, so that it has a repeating but non-terminating base-2 representation

`\frac13 = 0.010101\ldots_2`