Question

Evaluate (25/36)^1/2
A.25/6
B.5/36
C.25/36
D.5/6

Answer 1

5/6

Explanation:

Well we can use the exponential identity:
`((a)/(b))^n=(a^n)/(b^n)`

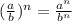
And the most intuitive explanation I have, is that the equation can also be represented as:
`(a)/(b) * (a)/(b)*(a)/(b)...\text{ n amount of times}`

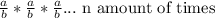
So simplifying this expression, by multiplying the numerators and denominators, you get:
`\frac{a*a*a...\text{ n amount of times}}{b*b*b...\text{ n amount of times}}`

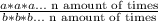
This is basically the definition of an exponent, so you can rewrite the equation as:
`(a^n)/(b^n)`

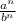
The next thing to know, is what the 1/2 exponent truly means. So we can generally represent any radical with root n, as the following:
`\sqrt[n]{a} = a^{(1)/(n)}`

The reason for this, is because of the exponent product rule, which just states:
`x^a*x^b=x^(a+b)`

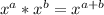
And I think the most intuitive explanation to this, is the equation can be represented as:
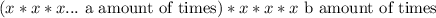`(x*x*x...\text{ a amount of times}) * x*x*x\text{ b amount of times}`, so there are "a" x's being multiplied by each other, and "b" x's being multiplied by each other, so we can combine these, and the total amount of x's being multiplied will be a+b

To give an example, let's take the following equation:
`x^3*x^2` which can be represented as:
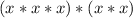`(x*x*x)*(x*x)` in total there are 5 x's being multiplied by each other which can be represented as:
`x^5`

Ok so the reason I'm explaining this,
`a^{(1)/(n)} * a^{(1)/(n)}*a^{(1)/(n)}...\text{ n amount of times} = a^{(1)/(n)*n} =a^1=a`

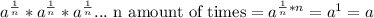
Now this may be a bit confusing to look at first, but the general idea is if you have a number:
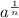`a^{(1)/(n)}` and multiply it out "n" amount of times by it self, you will get the number "a". That sounds familiar doesn't it? That's basically what an "nth root is"

So in our specific case, we have the square root:
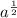`a^(1)/(2)`, now if we multiplying it by it self, we get:
`a^(1)/(2)*a^(1)/(2)=a^{(1)/(2)+(1)/(2)}=a^{(2)/(2)}=a^1=a`

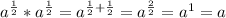
So if we take a^1/2 and multiply it by it self, we get "a", which means that a^1/2 is really just the square root of "a"

So now distributing the exponent using the previous identity discussed as well as what the 1/2 exponent really represents, we get the expression:
`(√(25))/(√(36)) = (5)/(6)`