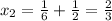Answer:
The two roots of the quadratic equation are
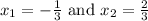
Explanation:
Original quadratic equation is
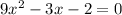
Divide both sides by 9:
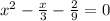
Add
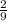 to both sides to get rid of the constant on the LHS
to both sides to get rid of the constant on the LHS
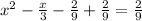 ==>
==>
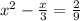
Add
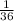 to both sides
to both sides

This simplifies to
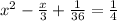
Noting that (a + b)² = a² + 2ab + b²
If we set a = x and b =
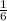 we can see that
we can see that
 =
=
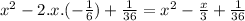
So
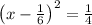
Taking square roots on both sides
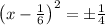
So the two roots or solutions of the equation are
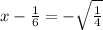 and
and
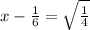
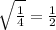
So the two roots are
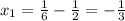
and