Question

What is the inverse

Answer 1

Third choice

`(√(2x))/(2) + 5, x\ge0`

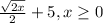
Explanation:

Definition

An inverse function is defined as a function, which can reverse into another function.

Thus, if we have a function f(x) which evaluates to k at x = a or in other words f(a) = k, then the inverse of that function indicated by f⁻¹(x) will be such that f⁻¹(k) = a. This is the same as stating that f⁻¹(f(a)) = a

In order the find the in verse of a function f(x) the following are the steps

• Set y = f(x)
• Switch x and y
• Solve for y

Given
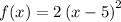`f(x) = 2 \left(x - 5\right)^(2)`, set it equal to y

`y=2 \left(x - 5\right)^(2)`

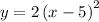
Swap the variables x and y

`x=2 \left(y - 5\right)^(2)` ==>
`(x - 5)^2 = (x)/(2)`

`x - 5 = \pm \sqrt(x)/(2)}\\\\x = \pm \sqrt(x)/(2)} + 5\\\\`

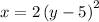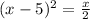
Solve for y. There are two possible solutions

`y= (√(2) √(x))/(2) + 5 = (√(2x))/(2) + 5`

`y=- (√(2) √(x))/(2) + 5` =
`- (√(2x))/(2) + 5`

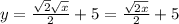
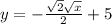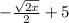
The only matching choice are choices 1 and 3. In order to determine if it is the first or the third, plug in 0 and see if the inverse value results in a real number

Substituting 0 for x in
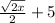`(√(2x))/(2) + 5` gives us 0 + 5 = 5 which is a valid real

So the domain of the function are all values ≥ 0

Hence choice 3, not choice 1