The equation of the line passes through the point
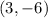 and has a slope
and has a slope
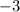 is
is
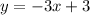 .
.
What are a line and the slope of a line?
Line:
- A line has only one dimension i.e., length and no width.
- It is formed with an infinite number of points lying on it.
- It can be extended infinitely along a straight path in both directions.
- An infinite number of lines pass through a given point, and a unique straight line can be drawn if any two points on that line are shown.
The slope of a line:
The slope of a line is the tangent value of the angle
 i.e.,
i.e.,
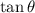 , where
, where
 is the angle made by the line with the positive
is the angle made by the line with the positive
 -axis.
-axis.
Equation of a line:
The equation of a line in slope-intercept form is given by
 , where
, where
 is the slope of the line and
is the slope of the line and
 is the
is the
 intercept of the line.
intercept of the line.
Here, we want to find the equation of the line which passes through the point
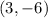 and has a slope
and has a slope
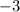 .
.
So, put
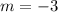 in
in
 and obtain
and obtain
 .
.
Now, since the line passes through the point
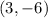 , put
, put
 and
and
 in
in
 to obtain:
to obtain:
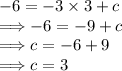
Therefore, after substituting
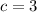 in
in
 , we obtain the required equation of the line that is
, we obtain the required equation of the line that is
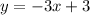 .
.
So, the equation of the line that passes through the point
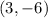 and has a slope
and has a slope
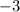 is
is
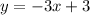 .
.