Question

Given the functions f(x) = log2(4x) and g(x) = 4^x – 3, which of the following statements is true? (just the x is the exponent, its 4 raised to the power of x, minus 3)

Both f(x) and g(x) have a common domain on the interval (0, ∞).
Both f(x) and g(x) have the same range of (–∞, 0].
Both f(x) and g(x) have the same intercept of (2, 0).
Both f(x) and g(x) increase on the interval of (–4 , ∞).

Answer 1

Option A

Explanation:

#Domain

f(x) is logarithm function so domain is positive

• (0,oo) is correct

g(x) has the domain R i e(-oo,oo)

So they both have common domain as (0,oo)

#Range

f(x) has domain R

g(x) is 4^x-3

Asymptote is present at y=0-3 i e y=3

So range is

• (-3,oo)

Not same range

#x intercept

log_2(4x):-

• log_2(4x)=0
• 4x=e⁰
• 4x=1
• x=1/4

4^x-3

• 4^x-3=0
• 4^x=3
• xlog4=log3
• x=log3/log4
• x=0.79

Not same

#y intercept

First one is logarithm function, -4 is not in its domain so undefined .

• False

Answer 2

Both f(x) and g(x) have a common domain on the interval (0, ∞).

Explanation:

Given functions:

`\begin{cases}f(x)=\log_2(4x)\\ g(x)=4^x-3 \end{cases}`

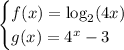
Domain

The domain of a function is the set of all possible input values (x-values).

Since we cannot take logs of negative numbers or zero, the domain of function f(x) is (0, ∞).

The domain of function g(x) is unrestricted and therefore (-∞, ∞).

Therefore, both functions have a common domain on the interval (0, ∞) since the domain (0, ∞) is part of (-∞, ∞).

Range

The range of a function is the set of all possible output values (y-values).

The range of f(x) is unrestricted and therefore (-∞, ∞).

The parent function of g(x) is
`y=4^x`. This has a range of (0, ∞) as it has an asymptote at y = 0. Therefore, as g(x) is translated 3 units down, g(x) will have an asymptote at y = 3.

Therefore, the range of g(x) is (-3, ∞).

So f(x) and g(x) do not have the same range.

x-intercept

The x-intercept is when the curve crosses the x-axis, so when y = 0.

To find if the x-intercept of both functions is at x = 2, substitute this value into the functions and solve for y:

`\begin{aligned}f(2) & =\log_2(4 \cdot 2)\\ & = \log_28\\ & = \log22^3\\ & = 3\log_22\\ & =3\end{aligned}`

`\begin{aligned}g(2) & =4^2-3\\ & = 4 \cdot 4 - 3\\& =16-3\\ & =13\end{aligned}`

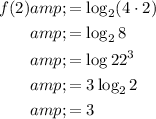
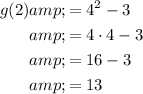
Therefore, f(x) and g(x) do not have an x-intercept at x = 2.

Increase on interval (–4 , ∞)

As the domain of f(x) is (0, ∞), it is undefined over the interval (-4, 0] and therefore is not increasing on the interval (-4, ∞).