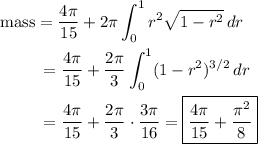Question

Write an integral in cylindrical coordinates for the mass of the solid with density p(x, y, z) = z√(x² + y²) that lies inside the sphere x² + y² + (z − 1)² = 1 and above the cone z = √(x² + y²)​

Answer 1

To get the mass, we integrate the density function over the given region.

In cylindrical coordinates, the sphere has equation

`x^2 + y^2 + (z-1)^2 = 1 \implies (z-1)^2 = 1-r^2 \implies z = 1 \pm √(1-r^2)`

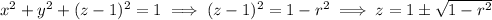
The region of interest lies below the top half of the sphere, so that
`z\le1+√(1-r^2)`.

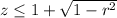At the lower end, the cone has equation, and hence
`z` has lower limit,

`z = √(x^2+y^2) = √(r^2) = r`

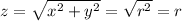
The upper hemisphere and cone meet when

`1 + √(1 - r^2) = r \implies 1-r^2 = (r-1)^2 \implies 2r^2 - 2r = 0 \\\\ \implies r=0\text{ or } r=1`

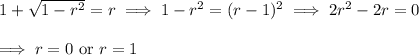
Then the mass of the given solid is

`\displaystyle \mathrm{mass} = \iiint_E z √(x^2+y^2) \, dV \\\\ ~~~~~~~~ = \int_0^(2\pi) \int_0^1 \int_r^(1+√(1-r^2)) r^2 z \, dz \, dr \, d\theta \\\\ ~~~~~~~~ = \pi \int_0^1 r^2 \left(\left(1+√(1-r^2)\right)^2 - r^2\right) \, dr \\\\ ~~~~~~~~ = 2\pi \int_0^1 (r^2 - r^4) \, dr + 2\pi \int_0^1 r^2 √(1-r^2) \, dr \\\\ ~~~~~~~~ = (4\pi)/(15) + 2\pi \int_0^1 r^2 √(1-r^2) \, dr`

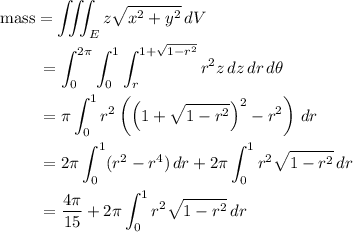
Integrate by parts.

`u = r \implies du = dr \\\\ dv = r √(1 - r^2) \, dr \implies v = -\frac13 (1-r^2)^(3/2)`

`\implies \displaystyle \int_0^1 r^2 √(1-r^2) \, dr = \frac13 \int_0^1 (1 - r^2)^(3/2) \, dr`

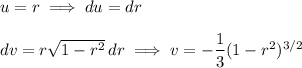
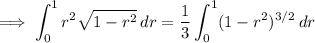
Substitute
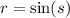`r=\sin(s)` and
`dr=\cos(s)\,ds`.

`\displaystyle \int_0^1 (1-r^2)^(3/2) \, dr = \int_0^(\pi/2) \cos^4(s) \, ds \\\\ ~~~~~~~~ = \int_0^(\pi/2) \left(\frac{1 + \cos(2s)}2\right)^2 \, ds \\\\ ~~~~~~~~ = \frac14 \int_0^(\pi/2) (1 + 2\cos(2s) + \cos^2(2s)) \, ds \\\\ ~~~~~~~~ = \frac14 \int_0^(\pi/2) \left(1 + 2\cos(2s) + \frac{1+\cos(4s)}2\right) \, ds \\\\ ~~~~~~~~ = \frac14 \int_0^(\pi/2) (1 + 2\cos(2s)) \, ds + \frac18 \int_0^(\pi/2) (1 + \cos(4s)) \, ds \\\\ ~~~~~~~~ = \frac\pi8 + \frac\pi{16} = (3\pi)/(16)`

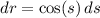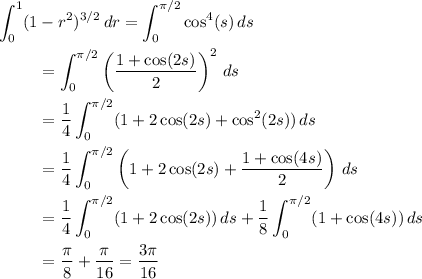
Putting it all together, the mass is

`\displaystyle \mathrm{mass} = (4\pi)/(15) + 2\pi \int_0^1 r^2 √(1-r^2) \, dr \\\\ ~~~~~~~~ = (4\pi)/(15) + \frac{2\pi}3 \int_0^1 (1 - r^2)^(3/2) \, dr \\\\ ~~~~~~~~ = (4\pi)/(15) + \frac{2\pi}3 \cdot (3\pi)/(16) = \boxed{(4\pi)/(15) + \frac{\pi^2}8}`