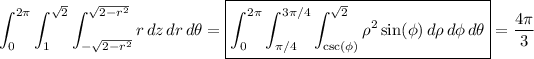Question

Rewrite the following integral in spherical coordinates.​

Answer 1

In cylindrical coordinates, we have
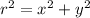`r^2=x^2+y^2`, so that

`z = \pm √(2-r^2) = \pm √(2-x^2-y^2)`

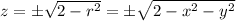
correspond to the upper and lower halves of a sphere with radius
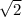`\sqrt2`. In spherical coordinates, this sphere is
`\rho=\sqrt2`.

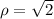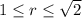`1 \le r \le \sqrt2` means our region is between two cylinders with radius 1 and
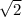`\sqrt2`. In spherical coordinates, the inner cylinder has equation

`x^2+y^2 = 1 \implies \rho^2\cos^2(\theta) \sin^2(\phi) + \rho^2\sin^2(\theta) \sin^2(\phi) = \rho^2 \sin^2(\phi) = 1 \\\\ \implies \rho^2 = \csc^2(\phi) \\\\ \implies \rho = \csc(\phi)`

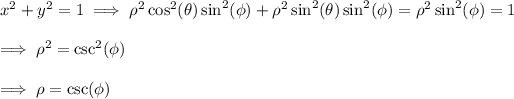
This cylinder meets the sphere when

`x^2 + y^2 + z^2 = 1 + z^2 = 2 \implies z^2 = 1 \\\\ \implies \rho^2 \cos^2(\phi) = 1 \\\\ \implies \rho^2 = \sec^2(\phi) \\\\ \implies \rho = \sec(\phi)`

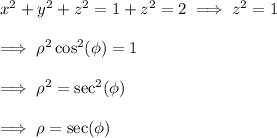
which occurs at

`\csc(\phi) = \sec(\phi) \implies \tan(\phi) = 1 \implies \phi = \frac\pi4+n\pi`

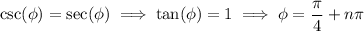
where
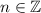`n\in\Bbb Z`. Then
`\frac\pi4\le\phi\le\frac{3\pi}4`.

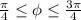The volume element transforms to

`dx\,dy\,dz = r\,dr\,d\theta\,dz = \rho^2 \sin(\phi) \, d\rho \, d\theta \, d\phi`

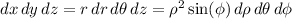
Putting everything together, we have

`\displaystyle \int_0^(2\pi) \int_1^(\sqrt2) \int_(-√(2-r^2))^(√(2-r^2)) r \, dz \, dr \, d\theta = \boxed{\int_0^(2\pi) \int_(\pi/4)^(3\pi/4) \int_(\csc(\phi))^(\sqrt2) \rho^2 \sin(\phi) \, d\rho \, d\phi \, d\theta} = \frac{4\pi}3`