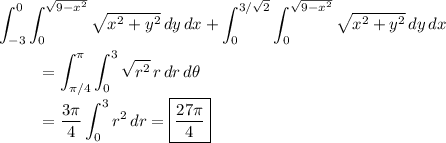The domain of integration is a circular sector subtended by an angle of 3π/4 radians, belonging to a circle of radius 3.
The first integral is taken over the left half of the upper semicircle.
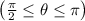
The second integral is taken over a sector belonging to the right half of the same semicircle. Notice that the line
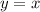 meets the semicircle
meets the semicircle
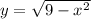 when
when
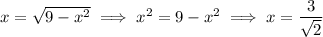
and the line
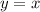 makes an angle of π/4 with the positive
makes an angle of π/4 with the positive
 -axis.
-axis.
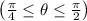
Then the two integrals combine into one integral in polar coordinates, and