The
 -coordinate of the center of mass is the average value of
-coordinate of the center of mass is the average value of
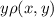 over the plate, given by the ratio of the integral of
over the plate, given by the ratio of the integral of
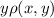 to the mass of the plate.
to the mass of the plate.
The mass of the plate is

while the integral of
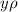 over the plate is
over the plate is
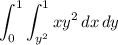
and the
 -coordinate of the center of mass is
-coordinate of the center of mass is
