Question

Which equation represents an inverse variation function that passes through the points (4, 5) and (10, 2)?

O y=x
O y = 5
4x
O y = 20x
0 y = 20
X

Answer 1

An inverse variation function has the following form:

`y=(k)/(x )`

where is constant.

Because the function traverses (4, 5). therefore

5
`5=(k)/(4)`

`k=20`

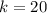
As a result, the required function is

`y=(20)/(x)`

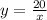
or

`xy=20`
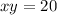
Check that the function is correct by passing it through the point (10, 2).

When x = 10, get

`y=(20)/(10) =2`

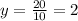
This confirms that the function is correct.

Answer:
`y=(20)/(x) or xy=20`

I hope this helps.