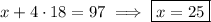The arc VQRST spans half the circle, so it measures 180 degrees. It's made up of the minor arcs VQ, QR, RS, and ST, so their measures all add up to 180 degrees.
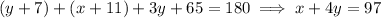
The arc QRS is subtended by a right angle, so it measures 90 degrees. It's made up of arcs QR and RS, so
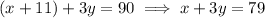
Solve for
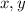 . Eliminating
. Eliminating
 , we have
, we have
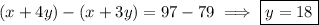
Substituting this into either equation, we find