Question

Twelve seconds after starting from rest a freely-falling cantaloupe has a speed of?

Answer 1

117.6 m/s

Step-by-step explanation:

The formula of free-falling velocity is:

`\displaystyle{v = u + gt}`

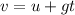
where u is initial velocity, g is gravitational force (defined to be 9.8 m/s^2) and t is time.

Since cantaloupe does not have initial velocity then u will equal to 0 which makes the equation to:

`\displaystyle{v = gt}`

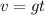
Since cantaloupe is free-falling and has its direction or motion same as gravitational force. Therefore, g = 9.8 m/s^2 and t = 12:

`\displaystyle{v = 9.8 * 12}\\\\\displaystyle{v = 117.6 \ \, \sf{m/s}}`

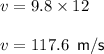
Since distance and displacement have same magnitude in this case with positive value then speed will equal to velocity in sign (positive/negative).

Hence, speed for free-falling cantaloupe after 12 seconds will be 117.6 m/s