Question

Pyramid AAA has a triangular base where each side measures 444 units and a volume of 363636 cubic units. Pyramid BBB has the same height, but each side of its base is 666 units long.

Answer 1

Pyramid BBB's height is 12.77972623 and its volume = 818181.0001

Explanation:

Let's solve for the height of triangle AAA and then solve for the volume of BBB.

We know that the formula to solve for the volume of a pyramid is:

V = 1/3(area of the base)(height)

Since both Pyramid AAA and BBB have triangular bases, we know that we must first find the area of the base, which for a triangle is:

1/2 (base)(height)

Let's begin with Pyramid AAA:

Since all three sides measure 444 units, we know the triangle has 3 equal sides, which means its equilateral. This means we know the base = 444 units.

To find the height, we divide the triangle in half and we are given a 30-60-90 special right triangle, and the height, which is the side opposite the 60° angle, is
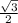`(√(3) )/(2)` times the hypotenuse. The hypotenuse is again, 444 units, so we multiply 444 times
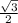`(√(3) )/(2)` to get 384.5152793, the height of the triangular base.

Now we can find the value of the base:

1/2 (384.5152793)(444) = 85362.392

Finally,

We find the height of the pyramid AAA:

1/3(85362.392)(h) = 363636

h = 363636/ (1/3)(85362.392)

h = 12.77972623

We finally found the height of Pyramid AAA, which is equal to the height of Pyramid BBB. Again, we find the height of the triangular base using the same process:

(1/2)666 · 666(
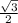`(√(3) )/(2)`) = 192065.382

Finally, we plug both the height and the area of the base to find the volume of Pyramid BBB:

1/3(192065.382)(12.77972623) = V

V = 818181.0001