Answer:
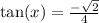
Explanation:
So an angle has two parts. Initial side and terminal side.
Inital side like on x axis. and terminal side shows how much it open up. Here the terminal angle terminates in second quadrant so we have the following
- A negative Cosine Value
- A positive Sine value
- A negative Tangent Value.
Now, using Pythagoras identity let solve for cos theta.
Here you on the right track but remeber that son theta=1/3 so sin theta squared would be 1/3 squared so we have


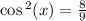
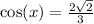
Note since cosine is negative in second quadrant, cos theta is

To find tan theta we do the following
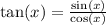
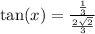
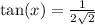
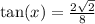

So
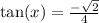
Tan is negative in second quadrant