Question

Given three squares of different areas, the perimeter of square A is 2/3 the perimeter of square B, and the perimeter of square B is 2/3 the perimeter of square C. If the area of square A is 16 square units, what is the area of square C?

Answer 1

81

Explanation:

Let a, b and c be the sides of the squares A, B and C respectively

Area of a square of side x = x²

Area of A = a² = 16

Area of C = c² to be determined

Perimeter of square A = 4a (perimeter of a square is 4 times side length)

Similarly perimeters of squares B and C are 4b and 4c respectively

We are given Perimeter of square A = (/3)(Perimeter of square B)

So,
`4a = (2)/(3) 4b\\`

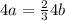
Dividing by 4 on both sides gives us a = 2b/3

Perimeter of square B = (2/3) x perimeter of square C

`4b = (2)/(3) 4c\\\\` ==> b = 2c/3

Using this relationship between a, b and c we can express a in terms of c and vice versa

`a = (2)/(3) b = ((2)/(3)) ((2)/(3) c) = (4)/(9) c`

`a^2 = ((4)/(9) c)^2 = (16)/(81) c^2 = 16\\` ==>
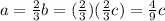
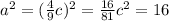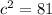`c^2 = 81\\` (Answer)

We can verify our answer as follows

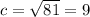`c = √(81) = 9\\` , perimeter of C = 4x = 36

Perimeter of b = (2/3) 36 = 24

Perimeter of a = (2/3)24 = 16 which is 4a