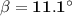Answer:
○
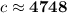
○

○
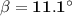
Explanation:
Use the attached diagram for help.
• To solve for c, we have to use the cosine rule, where:
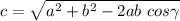
Substituting the values:
⇒
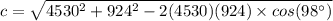
⇒
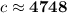
• Now that we know the value of c, we can use the sine rule to calculate the value of α (alpha):
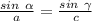
Substituting the values:
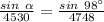
⇒
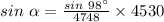
⇒
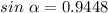
⇒

• Since we now have the values of both ∠α and ∠γ, we can find the value of ß using the triangle sum theorem:
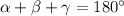
⇒
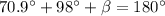
⇒
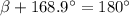
⇒

⇒