Question

Help math
look at pic​

Answer 1

Answer:
`\Large\boxed{(-4,~-3)~\text{and}~(-2,~1)}`

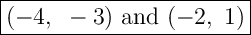
Explanation:

Given the system of equation

`1)~y=-(x+2)^2+1`

`2)~y=2x+5`

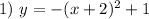
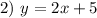
Expand the parenthesis of the 1) equation

`y=-(x+2)^2+1`

`y=-(x^2+4x+4)+1`

`y=-x^2-4x-4+1`

`y=-x^2-4x-3`

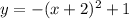
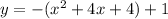
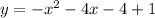
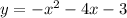
Current System

`1)~y=-x^2-4x-3`

`2)~y=2x+5`

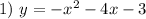
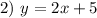
Substitute the y value of the 1) equation with the 2) equation

`2x+5=-x^2-4x-3`

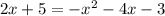
Add ( x² + 4x + 3) on both sides

`2x+5+(x^2+4x+3)=-x^2-4x-3+(x^2+4x+3)`

`2x+5+x^2+4x+3=0`

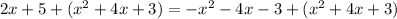
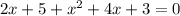
Combine like terms

`x^2+2x+4x+5+3=0`

`x^2+6x+8=0`

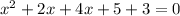
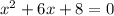
Factorize the quadratic equation

`(x+4)(x+2)=0`

`x=-4~\text{or}~x=-2`

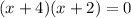
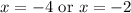
Substitute the x values into one of the equations to find the y value

`y=2x+5`

`y=2(-4)+5=-8+5=-3`

`y=2(-2)+5=-4+5=1`

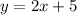
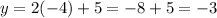
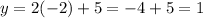
Therefore, the two solutions are:

`\Large\boxed{(-4,~-3)~\text{and}~(-2,~1)}`

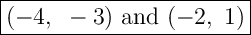
Hope this helps!! :)

Please let me know if you have any questions