A. The key features that describe this graph include:
A. domain: (-3, 4]
B. range: (-3, 3]
C. increasing: (-3, -1)
D. decreasing: (-1, 4)
E. positive: (-2, 2)
F. negative: (-3, -2), (2, 4).
B. The average rate of change over the interval [-2, 0] for the graph is 1.
Part A.
A range is the set of all real numbers that connects with the elements of a domain for any function, usually read from bottom to top.
A domain is the set of all real numbers (x-values) for which a particular relation or function is defined.
By critically observing the graph of this absolute value function, the domain (x-values from left to right) and range (y-values from bottom to top) are:
Domain = (-3, 4] or -3 < x ≤ 4
Range = (-3, 3] or -3 < y ≤ 3
For any given function, y = f(x), if the output value is increasing when the input value is increased, then, the function is an increasing function. However, if the output value is decreasing when the input value is increased, then, the function is a decreasing function.
Based on the definition above, this graph is increasing and decreasing over the following intervals;
increasing = (-3, -1)
decreasing = (-1, 4)
Since the y-values are greater than 0 over the interval (-2, 2), then this function is positive on this interval. Also, the function is negative over the intervals (-3,-2) and (2, 4) because the y-values are less than 0.
Part B.
The average rate of change of a function f(x) on a closed interval [a, b] can be calculated by using this formula:
Average rate of change =
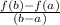
By critically observing the graph of the function f shown below, we can reasonably infer and logically deduce the following:
f(b) = f(0) = 2
f(a) = f(-2) = 0
Next, we would determine the average rate of change of the function over the interval [-2, 0]:
Average rate of change =
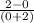
Average rate of change = 1.