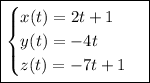Question

Find paremetric equations for the line through the point (1, 0, 1) and perpendicular to the vectors (3, 5, −2) and (2, 1, 0).​

Answer 1

Take the cross product of the given vectors to get one that is perpendicular to both of them.

`\langle 3, 5, -2 \rangle * \langle 2, 1, 0 \rangle = \langle 2, -4, -7 \rangle`

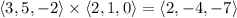
The line parallel to this vector and passing through the origin is given by the vector function

`\vec r(t) = \langle 2, -4, -7 \rangle t`

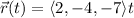
where
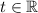`t\in\Bbb R`, and hence parametric equations

`\begin{cases}x(t) = 2t \\ y(t) = -4t \\ z(t) = -7t \end{cases}`

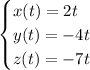
Translate this line by the vector
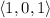`\langle1,0,1\rangle` to make it pass through the given point. So the line we want has vector function

`\vec r(t) = \langle 2, -4, -7 \rangle t + \langle 1, 0, 1 \rangle`

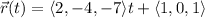
and parametric equations

`\boxed{\begin{cases} x(t) = 2t + 1 \\ y(t) = -4t \\ z(t) = -7t + 1 \end{cases}}`