Answer:
The prism has a volume about 340 cubic centimeters larger than the cone.
Explanation:
Cone
Formulas
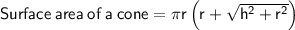

where:
- r = radius of circular base
- h = height perpendicular to the base
Given:
Substitute the given values into the formulas:

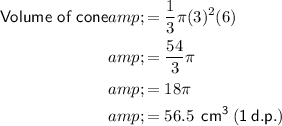
Prism
Formulas
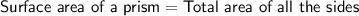
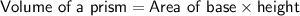
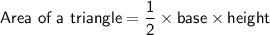
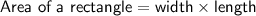
Given:
- Height of triangular base = 10 cm
- Base of triangular base = 8 cm
- Height of prism = 10 cm
Find the area of the triangular base of the prism:
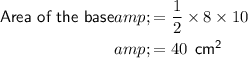
Find the third edge of the triangular base by using Pythagoras Theorem:
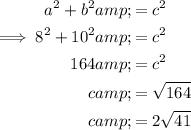
Use the found values and the formulas to find the surface area of volume of the prism:

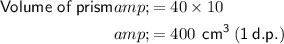
Conclusion
The surface area and volume of the prism is larger than that of the cone.
Difference between surface areas:
388.1 - 91.5 = 296.6 ≈ 300 cm²
Difference between volumes:
400 - 56.5 = 343.5 ≈ 340 cm³
Therefore:
- The prism has a surface area about 300 square centimeters larger than the cone.
- The prism has a volume about 340 cubic centimeters larger than the cone.