 lies in the second quadrant of the complex plane, so its argument is
lies in the second quadrant of the complex plane, so its argument is
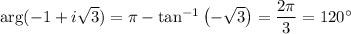
Then any sixth root of
 will have an argument of
will have an argument of
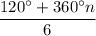
where
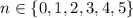 .
.
When
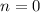 , we have
, we have
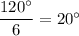
so D is a sixth root.
The other sixth roots are separated by arguments of 60 degrees (80, 140, 200, 260, and 320).