The second partial derivatives of
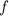 exist everywhere in its domain. By Schwarz's theorem, the mixed second-order partials derivatives are equal:
exist everywhere in its domain. By Schwarz's theorem, the mixed second-order partials derivatives are equal:
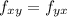
Then

We don't actually need to compute
 and
and
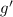 to know that they are both free of
to know that they are both free of
 . So when we differentiate for a second time with respect to
. So when we differentiate for a second time with respect to
 , the whole thing cancels out.
, the whole thing cancels out.