Let
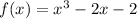 . Then differentiating, we get
. Then differentiating, we get
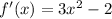
We approximate
 at
at
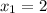 with the tangent line,
with the tangent line,
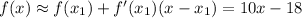
The
 -intercept for this approximation will be our next approximation for the root,
-intercept for this approximation will be our next approximation for the root,
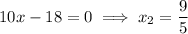
Repeat this process. Approximate
 at
at
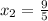 .
.
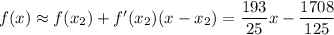
Then
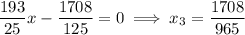
Once more. Approximate
 at
at
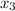 .
.
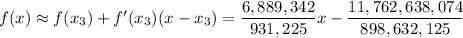
Then

Compare this to the actual root of
 , which is approximately 1.769292354, matching up to the first 5 digits after the decimal place.
, which is approximately 1.769292354, matching up to the first 5 digits after the decimal place.