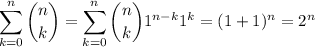Question

How many different ways are there to choose a subset of the set {1,2,3,4,5,6} so that the product of the members of the subset is even

Answer 1

You have to pick at least one even factor from the set to make an even product.

There are 3 even numbers to choose from, and we can pick up to 3 additional odd numbers.

For example, if we pick out 1 even number and 2 odd numbers, this can be done in

`\dbinom 31 \dbinom 32 = 3\cdot3 = 9`

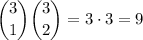
ways. If we pick out 3 even numbers and 0 odd numbers, this can be done in

`\dbinom 33 \dbinom 30 = 1\cdot1 = 1`

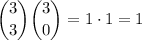
way.

The total count is then the sum of all possible selections with at least 1 even number and between 0 and 3 odd numbers.

`\displaystyle \sum_(e=1)^3 \binom 3e \sum_(o=0)^3 \binom 3o = 2^3 \sum_(e=1)^3 \binom3e = 8 \left(\sum_(e=0)^3 \binom3e - \binom30\right) = 8(2^3 - 1) = \boxed{56}`

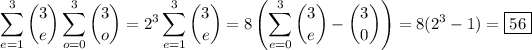
where we use the binomial identity

`\displaystyle \sum_(k=0)^n \binom nk = \sum_(k=0)^n \binom nk 1^(n-k) 1^k = (1+1)^n = 2^n`