Assuming a rectangular fenced area, let the area measure
 feet by
feet by
 feet. Then the length of fencing used is such that
feet. Then the length of fencing used is such that
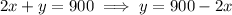
where
 is the length of the side parallel to the existing wall.
is the length of the side parallel to the existing wall.
The area enclosed by the fence is
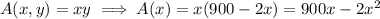
Find the critical points of
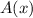 .
.
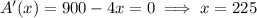
If two sides measure 225 feet, then the remaining side must measure
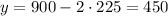
feet. So the pen must have dimensions 225-ft by 450-ft. We know this gives a maximum area, since by completing the square we find an upper bound for the enclosed area of

square feet.