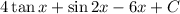Answer:
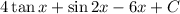
Explanation:
We are given the integral of:
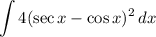
First, we can use a property to separate a constant out of integrand:
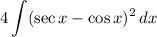
Next, expand the expression (integrand):
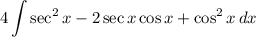
Since
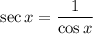 then it can be simplified to:
then it can be simplified to:

Recall the formula:
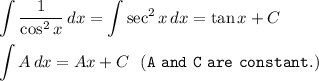
For
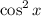 , we need to convert to another identity since the integrand does not have a default or specific integration formula. We know that:
, we need to convert to another identity since the integrand does not have a default or specific integration formula. We know that:

We can solve for
 which is:
which is:
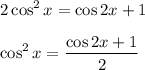
Therefore, we can write new integral as:
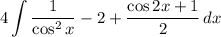
Evaluate each integral, applying the integration formula:
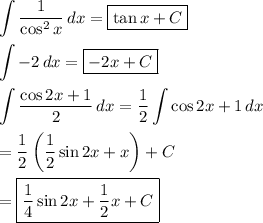
Then add all these boxed integrated together then we'll get:
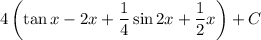
Expand 4 in the expression:
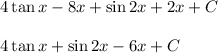
Therefore, the answer is: