Question

Determine over what interval(s) (if any) the mean value theorem applies.

y = ln(3x − 8)

Answer 1

(8/3, ∝)

Explanation:

Definition

The Mean Value Theorem states that for a continuous and differentiable function
`f(x)` on the closed interval [a,b], there exists a number c from the open interval (a,b) such that
`\bold{f'(c)=(f(b)-f(a))/(b-a)}`

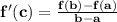
Note:

A closed interval interval includes the end points. Thus if a number x is in the closed interval [a, b] then it is equivalent to stating a ≤ x ≤ b.

An open interval does not include the end points so if x is in the open interval (a, b) then a < x < b

This distinction is important

The function is
`y = f(x)=\ln\left(3x-8\right)`

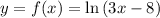
Let's calculate the first derivative of this function using substitution and the chain rule

Let

`u(x) = 3x-8\\\\(du)/(dx) = (d)/(dx)(3x-8) = (d)/(dx)(3x) - (d)/(dx)8 = 3 - 0 =3\\\\`

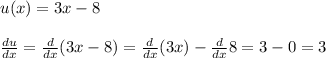
Substituting in the original function f(x), we get

`y = ln(u)\\\\dy/du = (1)/(u)`

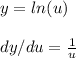
Using the chain rule

`(dy)/(dx)=(dy)/(du).(du)/(dx)`

We get

`(dy)/(dx)=(1)/(u)3=(1)/(3x-8)3=(3)/(3x-8)`

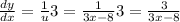
This has a real value for all values of x except for x = 8/3 because at x = 8/3, 3x - 8 = 0 and division by zero is undefined

Now
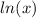`ln(x)` is defined only for values of x > 0. That means 3x-8 > 0 ==> 3x > 8 or x > 8/3

There is no upper limit on the value of x for ln(x) since ln(x) as x approaches ∝ ln(x) approaches ∝ and as x approaches ∝ 3/(3x-8) approaches 0

So the interval over which the mean theorem applies is the open interval (8/3, ∝)

At x = 8/3 the first derivative does not exist

Graphing these functions can give you a better visual representation