Answer:
Explanation:
This represents an arithmetic sequence, modeled by the formula
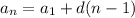 where a1 is the first term, d is the common difference, and n stands for the position in the sequence. For example, the number 27 is in the second position, so a2 = 27. We need to find the common difference, the same number either added in or subtracted away that will get us from one number to the next. To get from a1 = 19 to a2 = 27, we add 8. Then to get from 27 to 35 we add 8. Likewise, for the difference between 43 and 35. So d = 8. Our formula is
where a1 is the first term, d is the common difference, and n stands for the position in the sequence. For example, the number 27 is in the second position, so a2 = 27. We need to find the common difference, the same number either added in or subtracted away that will get us from one number to the next. To get from a1 = 19 to a2 = 27, we add 8. Then to get from 27 to 35 we add 8. Likewise, for the difference between 43 and 35. So d = 8. Our formula is
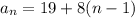 and simplify a bit to
and simplify a bit to
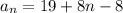 and a bit more to
and a bit more to

As you can see, arithmetic sequence formulas always represent straight lines!