Answer:
Explanation:
Use the midpoint formula to solve:
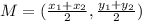
We know the midpoint and one set of coordinates, so filling those in:
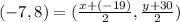
Since the -7 is the x coordinate of the midpoint, we set the x part of the equation equal to -7 and solve for x, and then do the same for y. The 2 equations are:
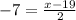 and
and
 We solve each one of these to get the x and y coordinates of the other endpoint. In both cases, multiply both sides of the equations by 2 and then solve by either adding or subtracting.
We solve each one of these to get the x and y coordinates of the other endpoint. In both cases, multiply both sides of the equations by 2 and then solve by either adding or subtracting.
-14 = x - 19 so
5 = x
16 = y + 30 so
-14 = y
The coordinates of the other endpoint are (5, -14)