Question

Find the sum of the first 16 terms of an arithmetic sequence where a4=7 and a7= 16.

Answer 1

`a_(4) = 7 \: \: \: \: \: \: \: \: \: \: \: \: a_(7) = 16`

`a_(4) = a_(1) + 3d \: \: \: \: \: \: \: \: \: a_(7) = a_(1) + 6d \\ 7 = a_(1) + 3d \: \: \: \: \: \: \: \: \: 16 = a_(1) + 6d`

`a_(1) + 3d = 7 \\ a_(1) +6 d = 16`

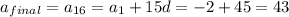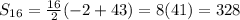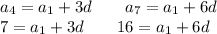
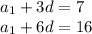
Solve the system

( a¹ , d ) = ( -2 , 3 )

So now we know that we are dealing with an arithmetic sequence of common difference 3 and first term -2, we will be using the formula for the sum of the terms

`S_(n) = (n)/(2) (a_(1) + a_(final))`

Where S is the sum

n is the number of terms that we're summing

a¹ is our first term of the sum

a(f) is final term in our sum

`a_(final) = a_(16) = a_(1) + 15d = - 2 + 45 = 43 \\`

`S_(16) = (16)/(2) ( - 2 + 43) = 8(41) = 328 \\`