Question

F (x) = 1/x-4 -6. Find the inverse of f (x) and it’s domain.

Answer 1

as you already know, to get the inverse of any expression we start off by doing a quick switcheroo on the variables and then solving for "y", let's do so.

`\stackrel{f(x)}{y}~~ = ~~\cfrac{1}{x-4}-6\qquad \stackrel{quick~switcheroo}{x~~ = ~~\cfrac{1}{y-4}-6}\implies x+6=\cfrac{1}{y-4} \\\\\\ y-4=\cfrac{1}{x+6}\implies \stackrel{f^(-1)(x)}{y}=\cfrac{1}{x+6}+4\qquad \qquad x\\e 4`

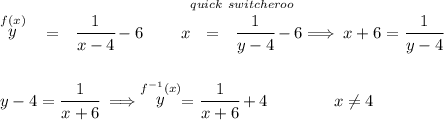
why "x" cannot ever be 4? well, if that ever happens, the denominator in our original equation will go poof, turn to 0 and thus the fraction will be undefined.