x + 3/x - 8 + 7/x-6=7/x-6
Variable x cannot be equal to any of the values 6.8 as division by zero is not defined. Multiply both sides of the equation by (x−8)(x−6), the lowest common denominator of x−8,x−6.
(x - 6)(x + 3) + (x - 8) × 7 = (x - 8) × 7
Use the distributive property to multiply x−6 by x+3 and combine like terms.
x² - 3x - 18 + ( x- 8) × 7 = (x - 8) × 7
Use the distributive property to multiply x−8 by 7.
x² - 3x - 18 + 7x - 56 = (x - 8) × 7
Combine −3x and 7x to get 4x.
x²+ 4x - 18 - 56 = (x - 8) × 7
Subtract 56 from −18 to get −74.
x² +4x - 74 = (x - 8) × 7
Use the distributive property to multiply x−8 by 7.
x² + 4x - 74 = 7x - 56
Subtract 7x on both sides.
x² + 4x - 74 - 7x = -56
Combine 4x and −7x to get −3x.
x² - 3x - 74= -56
Add 74 to both sides.
x² - 3x = - 56 + 74
Add −56 and 74 to get 18.
x² - 3x = 18
Divide −3, the coefficient of the x term, by 2 to get -3/2. Next, add the square of -3/2. to both sides of the equation. This step makes the left side of the equation a perfect square.
x² + 3x + (-3/2)² = 18 + (-3/2)²
Gets the square of − 3/2. To do this, find the square of the numerator and the denominator of the fraction.
x² + 3x + 9/4 = 18 + 9/4
Add 18 and 4/9.
x² + 3x + 9/4 + 81/4
Factor to x² + 3x + 9/4. In general, when x² + bx + c is a perfect square, it can always be factored as (x + b/2)².
( x - 3/2)² = 81/4
Take the square root of both sides of the equation.
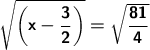
Simplify.
x - 3/2 = 9/2
x - 3/2 = - 9/2
Add 3/2 to both sides of the equation.
x = 6
x = -3
The variable x cannot be equal to 6.
x = -3