The total number of such groupings of 12 people into groups of 3, 4, and 5, regardless of Henry's placement, is
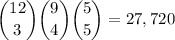
where
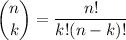
is the binomial coefficient. This is because we initially pick 3 people from the total 12, leaving 9 available; then 4 people from these 9, leaving 5 more; then the remaining 5 are all selected.
If Henry claims a spot in the group of 4, then we effectively can only pick 3 people from the 8 non-Henrys to get
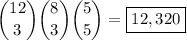
such groupings.