Answer:
-4568.25 m/s (2 d.p.)
Step-by-step explanation:
As we need to find the y-component of the initial velocity, consider the vertical and horizontal motion of the electron separately.
Trigonometry can be used to resolve the body's motion into its vertical and horizontal components:
- Horizontal component of u = u cos θ
- Vertical component of u = u sin θ
Vertical component of acceleration:
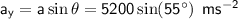
Vertical component of final velocity:
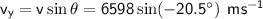

Therefore:
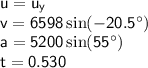
To find the vertical component of the initial velocity (u):
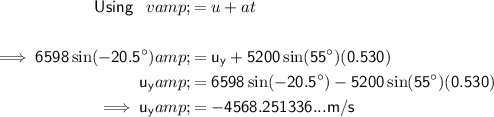
Therefore, the y-component (vertical component) of the initial velocity is -4568.25 m/s (2 d.p.).