1 Answer

Walv · Answer 1 · 2023-04-13T13:33:08+0000

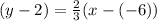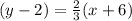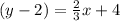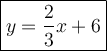$Answer:\large\boxed{y=(2)/(3) x+6}$

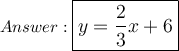
Explanation:

First let's convert 2x - 3y = 12 into
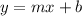y = mx + b form.

In order to do this, solve for y.

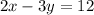
2x-3y=12

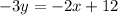
-3y=-2x+12

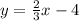
y=(2)/(3) x-4

This shows us that the slope is
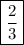
$\boxed{(2)/(3)}$

Now we use the point-slope formula:

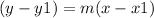
(y-y1)=m(x-x1)

where m is the slope and y1 and x1 are the point the line passes through

Using the point (-6,2) and slope, 2/3, we can find the equation:

(y-2)=(2)/(3) (x-(-6))

(y-2)=(2)/(3) (x+6)

(y-2)=(2)/(3) x+4

$\large\boxed{y=(2)/(3) x+6}$

Please log in or register to add a comment.