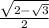Answer:
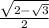
Explanation:
since 75 is half of 150, we can use the half angle formula of cos defined as:
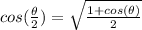 where theta=150
where theta=150
So plugging in the values we get:
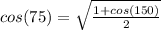
Now using the unit circle, we can solve for cos(150)

Now multiply the 1 by 2/2 to combine the numerator into one fraction

Combine the numerator into one fraction
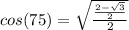
Keep, change, flip
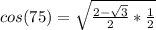
Multiply:
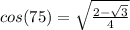
We can distribute the square root across the division:
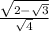
Simplify the denominator