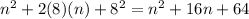Question

Fill in the blank to make the expression a perfect square:

n squared plus 16 n plus__(blank)__

Answer 1

64

Explanation:

So here you're just completing the square. the equation you gave is simply:
`n^2+16n+c` where c is the unknown value we're solving for. Whenever you complete the square, you add (b/2)^2

The reason for this, is because whenever you write a binomial as a perfect square it's in the form:
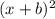`(x+b)^2` and this binomial expands out to become:
`x^2+2bx+b^2`

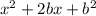
If we write the second term of the binomial as b/2 we get:

`(x+(b)/(2))^2=x^2+2((b)/(2))x+((b)/(2))^2`

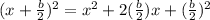
which simplifies to:

`(x+(b)/(2))^2=x^2+bx+((b)/(2))^2`

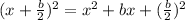
and as you can see the last term is (b/2)^2, which is why we need to add that part for it to be a perfect square.

So we would need to add (16/2)^2 = 8^2 = 64

This way, we can express it as a perfect square binomial:
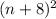`(n+8)^2` which expands out to:
`n^2+2(8)(n)+8^2 = n^2+16n+64`